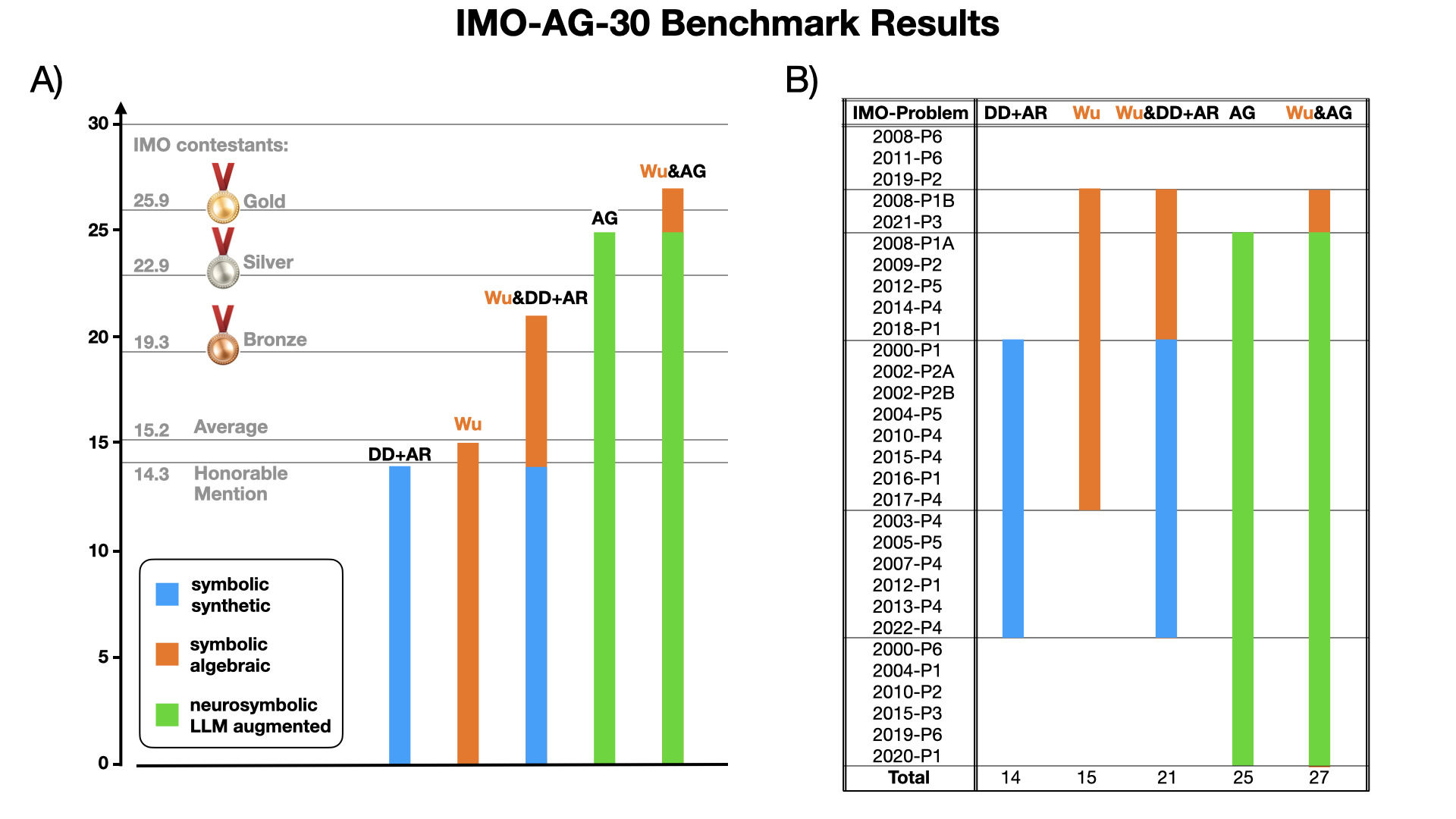
Proving geometric theorems constitutes a hallmark of visual reasoning combining both intuitive and logical skills. Therefore, automated theorem proving of Olympiad-level geometry problems is considered a notable milestone in human-level automated reasoning. The introduction of AlphaGeometry, a neuro-symbolic model trained with 100 million synthetic samples, marked a major breakthrough. It solved 25 of 30 International Mathematical Olympiad (IMO) problems whereas the reported baseline based on Wu’s method solved only ten.

 

In this paper, the IMO-AG-30 Challenge introduced with AlphaGeometry was revisited, and the researchers found that Wu’s method is surprisingly strong. Wu’s method alone can solve 15 problems, and some of them are not solved by any of the other methods. This leads to two key findings: (i) Combining Wu’s method with the classic synthetic methods of deductive databases and angle, ratio, and distance chasing solves 21 out of 30 methods by just using a CPU-only laptop with a time limit of 5 minutes per problem. Essentially, this classic method solves just 4 problems less than AlphaGeometry and establishes the first fully symbolic baseline, strong enough to rival the performance of an IMO silver medalist. (ii) Wu’s method even solves 2 of the 5 problems that AlphaGeometry failed to solve. Thus, by combining AlphaGeometry with Wu’s method a new state-of-the-art for automated theorem proving on IMO-AG-30, solving 27 out of 30 problems, the first AI method which outperforms an IMO gold medalist is finally achieved.

Read the full article at: arxiv.org